3. Représenter les nœuds en fonction des différents degrés de centralité
3.1. Degree centrality = A combien de personnes un compte peut accéder directement ?
3.2. Closeness centrality = en combien de temps un compte peut-il toucher l’ensemble du réseau ?
3.3. Betweenness centrality (Entremise ?) = quelle est la probabilité que cette personne soit l’itinéraire le plus direct entre deux personnes dans le réseau ?
3.4. « Centralité Eigenvector » = à combien de personnes bien connectées ce compte est-il connecté ?
3.5. Modularity class = identifier les relations entre les nœuds et mettre en avant des communautés
3.6. Aller plus loin dans l’analyse en combinant des filtres
Centralité relative des individus entre eux
Une caractéristique importante des réseaux est la centralité relative des individus entre eux. La centralité est une caractéristique structurelle des personnes dans le réseau, ce qui signifie que la centralité vous dit quelque chose sur la façon dont cette personne s’inscrit dans l’ensemble du réseau. Les personnes ayant des scores de centralité élevés sont souvent plus susceptibles d’être des leaders, des conduits d’information clés, et d’être les premiers à adopter tout ce qui se répand dans un réseau.
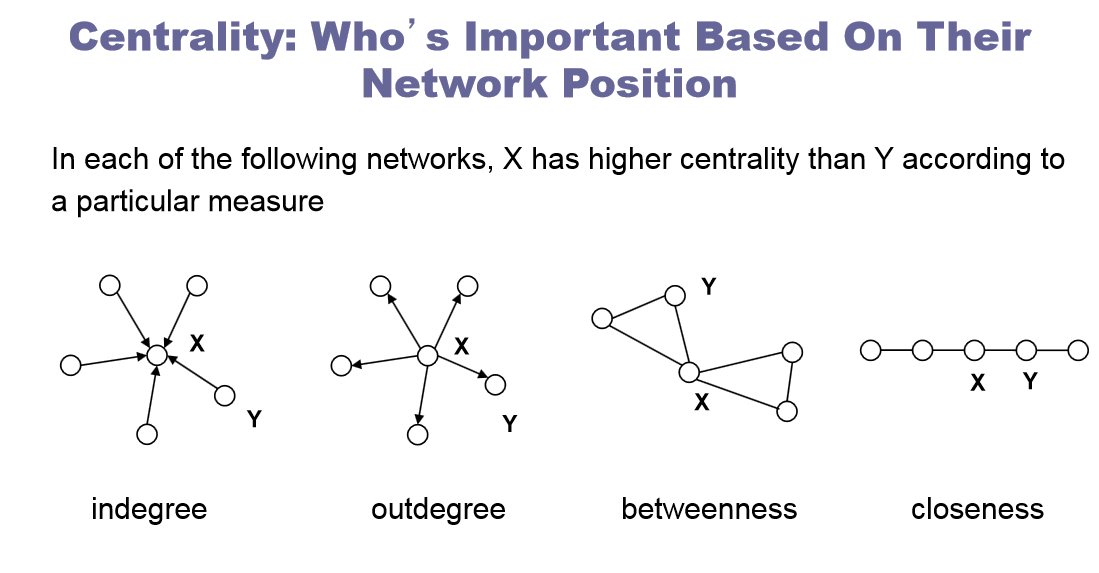
3.1. Degree Centrality = à combien de personnes un compte peut accéder directement ?
Connectivité locale
Les noeuds avec beaucoup de voisins sont centraux / Il s’agit du nombre de liens qui mènent vers ou en dehors du nœud. Il est utile pour évaluer les nœuds qui sont centraux par rapport à la diffusion de l’information et influencer leurs communautés.
Il faut noter que par défaut, le calcul de degré ne prend pas en compte le nombre de liens entre une entité A et une entité B : 15 liens (mentions, RT sur Twitter) tout comme 1 seul lien indiqueront un degré de relation. Il faut prendre en compte le poids, ou la pondération, via le calcul du "degré pondéré" sur Gephi (menu statistiques).
Le calcul de la centralité entrante pondérée (weighted in degree) donne un classement des comptes Twitter avec le plus de mentions. Le calcul de la centralité sortante pondérée (weighted out degree) classe les comptes twitter en fonction du nombre de tweets où ils ont mentionnés d’autres comptes (typiquement des spammeurs ou des comptes très actifs sur une thématique qui mentionnent des alliés ou des personnes influentes).
Cartographie des communautés autour de Vivatech 2019 sur le réseau Twitter :
Cartographie des communautés autour de Vivatech 2019 sur le réseau Instagram :
3.2. Closeness Centrality = en combien de temps un compte peut-il toucher l’ensemble du réseau ?
- Cette mesure traduit la distance sociale moyenne de chaque individu à tout autre individu dans le réseau. Elle calcule la longueur moyenne de tous les chemins les plus courts à partir d’un nœud à tous les autres nœuds dans le réseau.
- C’est une mesure de portée, c’est à dire la vitesse à laquelle l’information peut atteindre d’autres nœuds à partir d’un nœud de départ donné.
- En divisant 1 par le chemin du plus court moyen d’un individu à toutes les autres personnes dans le réseau, nous calculons leur centralité de proximité. De cette façon, une personne ayant un lien direct avec tout le monde finit avec un score de proximité de 1. Les personnes qui se connectent à la plupart des autres par de nombreux intermédiaires vont obtenir des scores proximité qui sont de plus en plus proche de zéro.
- La proximité de centralité tend à donner des scores élevés aux personnes qui sont près du centre de grappes locales (aka communautés de réseau) dans un réseau global plus important.
Applications
Les comptes à haute proximité de centralité ont tendance à être des influenceurs importants au sein de leur communauté de réseau local. Ils sont souvent des personnalités publiques au sein d’une communauté, d’une profession. Ils sont souvent respectés localement et ils occupent les chemins courts pour diffuser les informations au sein de leur communauté en réseau.
Mesure proche ou « Weighted Clustering Cofficient »
Le « Weighted Clustering Cofficient ». Cette mesure permet de calculer, en modérant en fonction de l’intensité des liens entre les nœuds (donc du nombre de mentions entrantes et sortantes) si les relations des nœuds proches d’un nœud A donné sont toutes connectées entres elles.
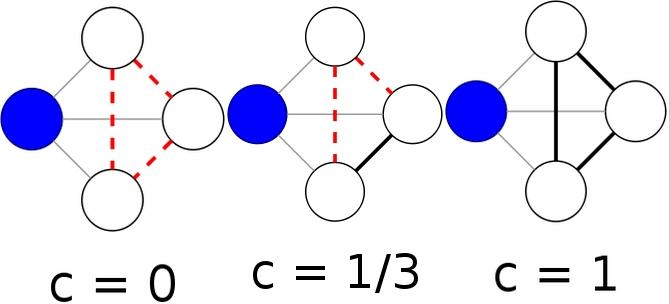
Cette mesure peut donc servir à préciser la closeness centrality en identifiant les nœuds et morceaux des réseaux les mieux connectés par communautés (et donc pour l’analyse Twitter savoir si certaines communautés s’appuient sur quelques comptes qui se mentionnent les uns les autres ou alors des ensembles de comptes connectés uniquement via des relations distantes). On parle d’un effet « small world », c’est-à-dire que les membres d’une communauté donnée vont être reliés par un ensemble de petits réseaux locaux interconnectés entre eux.
Exemples :
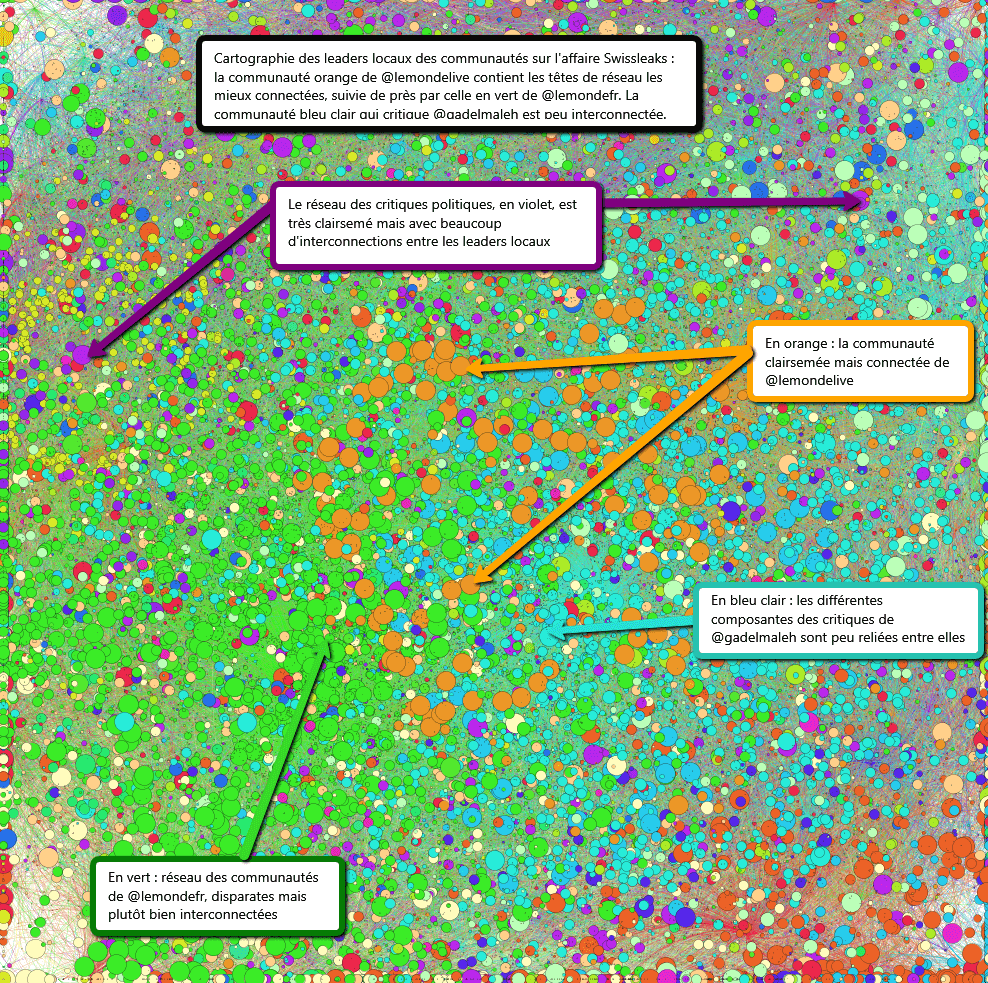
A comparer avec :

La cartographie N°2 (closeness centrality) montre une prédominance des leaders locaux de réseaux dans les communautés vertes (@lemondefr), orange (@lemondelive) et bleu clair (@gadelmaleh), et une dispersion des leaders violets (critique politique du swissleaks).
La première cartographie permet de pondérer les résultats et de mieux expliquer la répartition de l’influence des différents groupes (voir calculs suivants). Bien que moins importantes en terme de comptes twitter et de total de mentions, les communautés violettes et oranges obtiennent une certaine influence parce que leurs leaders locaux sont très fortement connectés.
3.3. Betweenness Centrality (Centralité) = quelle est la probabilité que cette personne soit l’itinéraire le plus direct entre deux personnes dans le réseau ?
Connectivité
Noeuds sur des lieux de passage sont centraux / Et donc de détecter les nœuds les plus susceptibles d’être dans des voies de communication entre les autres nœuds. Également utile pour déterminer les points où le réseau se briserait.
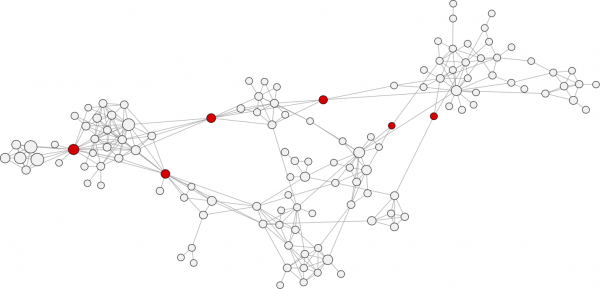
Il s’agit d’une mesure dérivée de la notion de décompte des chemins les plus courts entre les individus dans un réseau. Pour calculer la centralité intermédiaire, on commence par trouver tous les chemins les plus courts entre deux individus dans le réseau. Vous comptez alors le nombre de ces plus courts chemins qui passent par chaque individu. Ce nombre correspond à la centralité intermédiaire.
Ce calcul permet d’identifier les individus qui sont des conduits nécessaires à l’information qui doit traverser des éléments disparates de réseau. Ce sont généralement des personnes très différentes de celles avec une grande proximité. Les individus à forte Betweenness centrality (ou centralité) ne sont souvent pas le chemin le plus court pour joindre tout le monde, mais ils ont le plus grand nombre de chemins les plus courts qui vont nécessairement passer par eux.
Dans un réseau social, les individus avec un score élevé de centralité se trouvent souvent aux intersections des communautés de réseau plus densément connectés.
Applications
En raison de leurs emplacements entre les communautés de réseau, ces comptes à forte Betweenness centrality sont naturellement des courtiers d’information.

La mesure de la Betweeness centrality permet d’identifier plus facilement des réseaux activistes, utiles pour faire passer un message mais pas toujours visibles en termes de mentions.
3.4. « Centralité Eigenvector » = à combien de personnes bien connectées ce compte est-il relié ?
Cette analyse statistique permet de déterminer l’importance d’une personne au sein d’un réseau, et donc d’attribuer des valeurs à chaque personne de votre réseau. Une fois cette statistique calculée, vous pouvez aller sur le panneau de classement en haut à droite, et affecter une taille en fonction du paramètre « eigencentrality ». Vos données doivent être entre une taille minimum de 10 et maximum de 50. Utile pour déterminer qui est connecté aux nœuds les plus connectés.
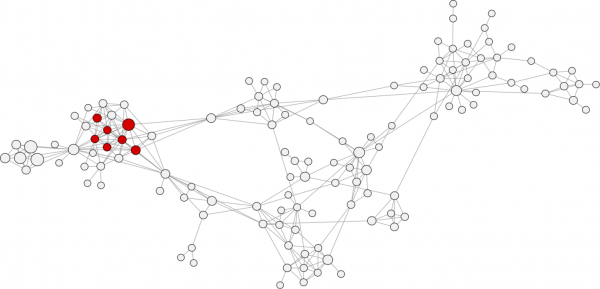
Cette mesure désigne essentiellement le fait qu’un individu est un compte autoritaire connecté à d’autres comptes autoritaires au sein d’un vaste réseau. Eigenvector centralité est calculée en évaluant la façon dont un individu est relié aux parties du réseau avec la plus grande connectivité. Les personnes ayant des scores élevés de vecteurs propres ont de nombreuses connexions, et leurs connexions ont de nombreuses connexions, et leurs connexions ont de nombreuses connexions… jusqu’au bout du réseau.
Applications
Les individus possédant un vecteur propre de centralité élevé sont considérés comme les leaders du réseau. Ce sont souvent des personnalités publiques avec de nombreux liens avec d’autres personnes à haut profil. Ainsi, ils jouent souvent des rôles de leaders d’opinion clés et façonnent la perception du public. Un exemple de cela est l’algorithme page rank de Google, qui est étroitement liée au vecteur propre de centralité calculé sur des sites Internet basés sur les liens pointant vers eux.
Ces comptes ne peuvent cependant pas effectuer nécessairement les rôles de haute proximité et intermédiarité. Ils n’ont pas toujours la plus grande influence locale et peuvent avoir un potentiel de courtage limitée. Comme un roi à l’écart dans sa cour ou le directeur général dans sa salle de réunion , ils peuvent parfois être isolés des individus et des communautés périphériques de réseau de petite taille qui ont une connectivité limitée avec les parties les plus densément connectés du réseau.
Les Hubs concentrent les liens sortants. Ils correspondent à des comptes chargés de redistribuer l’information à une communauté. Les Autorités centralisent les liens entrants. Ces liens se traduisent par des mentions, des sollicitations ou des références à un compte source.
3.5. Modularity Class = identifier les relations entre les nœuds et mettre en avant des communautés
Le filtre statistique Modularity Class est disponible dans l’onglet statistique à droite, qui s’appelle plus communément modularité. Il va détecter automatiquement si des personnes de votre réseau semblent liées entre elles. Ce calcul est pertinent à partir de plusieurs milliers de relations. Ce filtre va déterminer les communautés à l’intérieur du graphe, c’est à dire des ensembles de sommets fortement reliés entre eux, ce qui revient, dans la majeure partie des cas, à déterminer des groupes d’individus qui ont tendance à se retweeter, à s’interpeller ou à se mentionner.
Modularité (Newman 2004)
Nombre de liens dans chaque groupe moins le nombre de liens dans les mêmes groupes, dans un graph ou les liens auraient été redistribués de façon aléatoire. Trouver les communautés dans un graph = définir des groupes de façon à ce que le score de modularité soit le plus élevé.
Pour afficher cette information sur la carte, vous devez vous rendre par la suite dans l’onglet partition en haut à gauche, et sélectionner la statistique que vous avez créée, « modularity class ». En appliquant cette partition, les couleurs de votre réseau vont se modifier, et mettre en avant les relations entre les personnes. question game Il peut être utile de modifier les couleurs par défaut, Gephi ayant tendance à choisir des couleurs sombres assez semblables pour les principales communautés, ce qui peut engendrer des confusions.
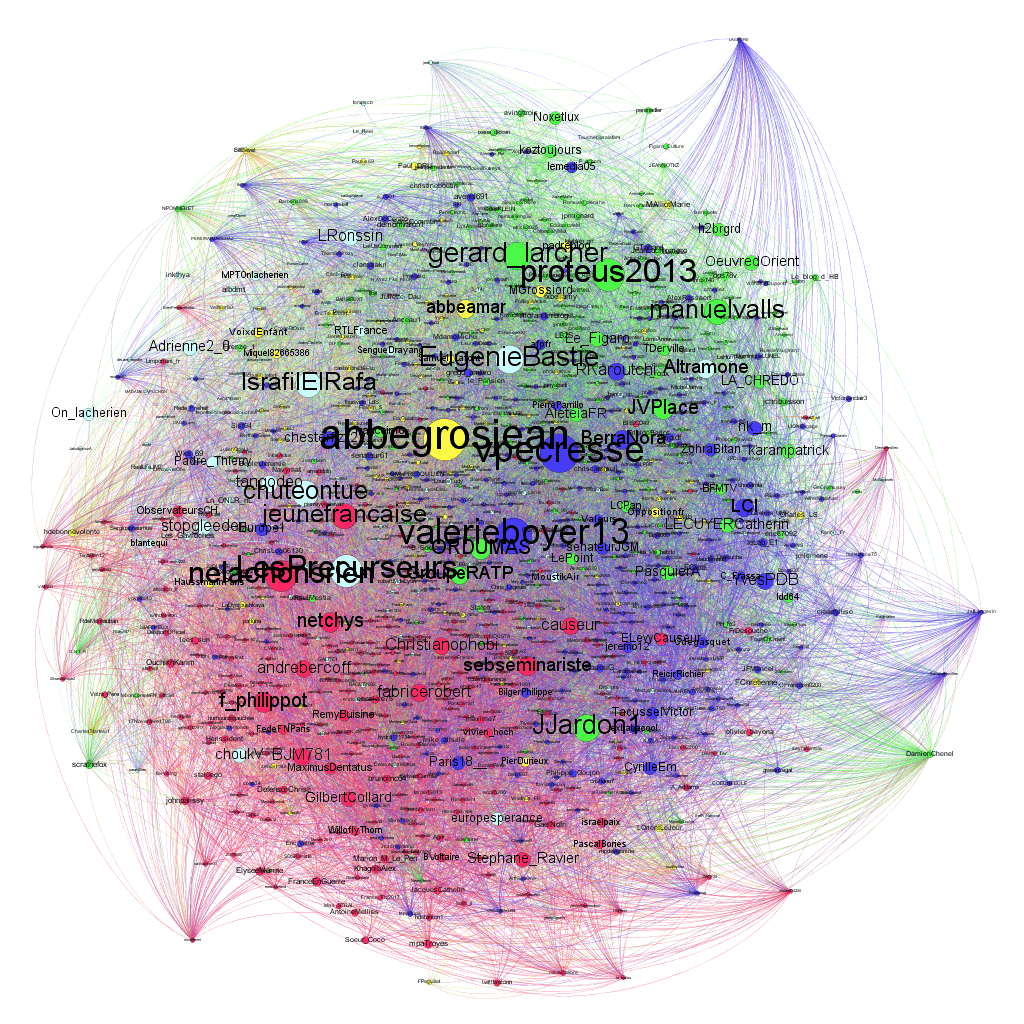
Comme le présente la cartographie ci-dessous correspondant au buzz contre la RATP après le retrait d’affiches de publicité soutenant les chrétiens d’orient, après calcul et utilisation du filtre, la modularité met en évidence 4 espaces de conversation distincts :
- vert : sphère “institutionnelle” : responsables politiques et religieux et leurs correspondants ;
- bleu : leaders d’opinion ancrés à droite et leurs correspondants ;
- bleu clair : militants catholiques radicaux et leurs correspondants ;
- jaune : abbés Grosjean et Amar et leurs correspondants ;
- rose : leaders d’opinion d’extrême-droite et leurs correspondants.
3.6. Aller plus loin dans l’analyse en combinant des filtres
| Faible nombre de mentions | Faible score de proximité | Faible centralité dans le réseau | |
| Fort nombre de mentions | X | Compte twitter membre d’un cluster éloigné du réseau | Connections du compte twitter redondantes et ne passant pas par lui |
| Fort score de proximité | Compte twitter relié à des comptes très actifs ou influents | X | Compte twitter relié à plusieurs autres comptes mais pas central |
| Forte centralité dans le réseau | Compte twitter essentiel pour la diffusion à certaines communautés | Compte twitter sert de lien exclusif entre le reste du réseau et un cluster | X |
Il est également possible via les filtres de Gephi de combiner des calculs statistiques, pour raffiner les résultats obtenus et identifier des comptes twitter aux propriétés spécifiques.
Exemple
Croisement entre le filtrage des comptes twitter les plus mentionnés et la variation de leur taille par valeur de betweeness centrality sur les tweets français de SwissLeaks :

On voit sur la cartographie des comptes les plus mentionnés que le compte @gadelmaleh est très mentionné, tout comme celui du @mondefr. Mais est-il central dans les discussions, et surtout est-il à l’origine lui-même de ces mentions ?
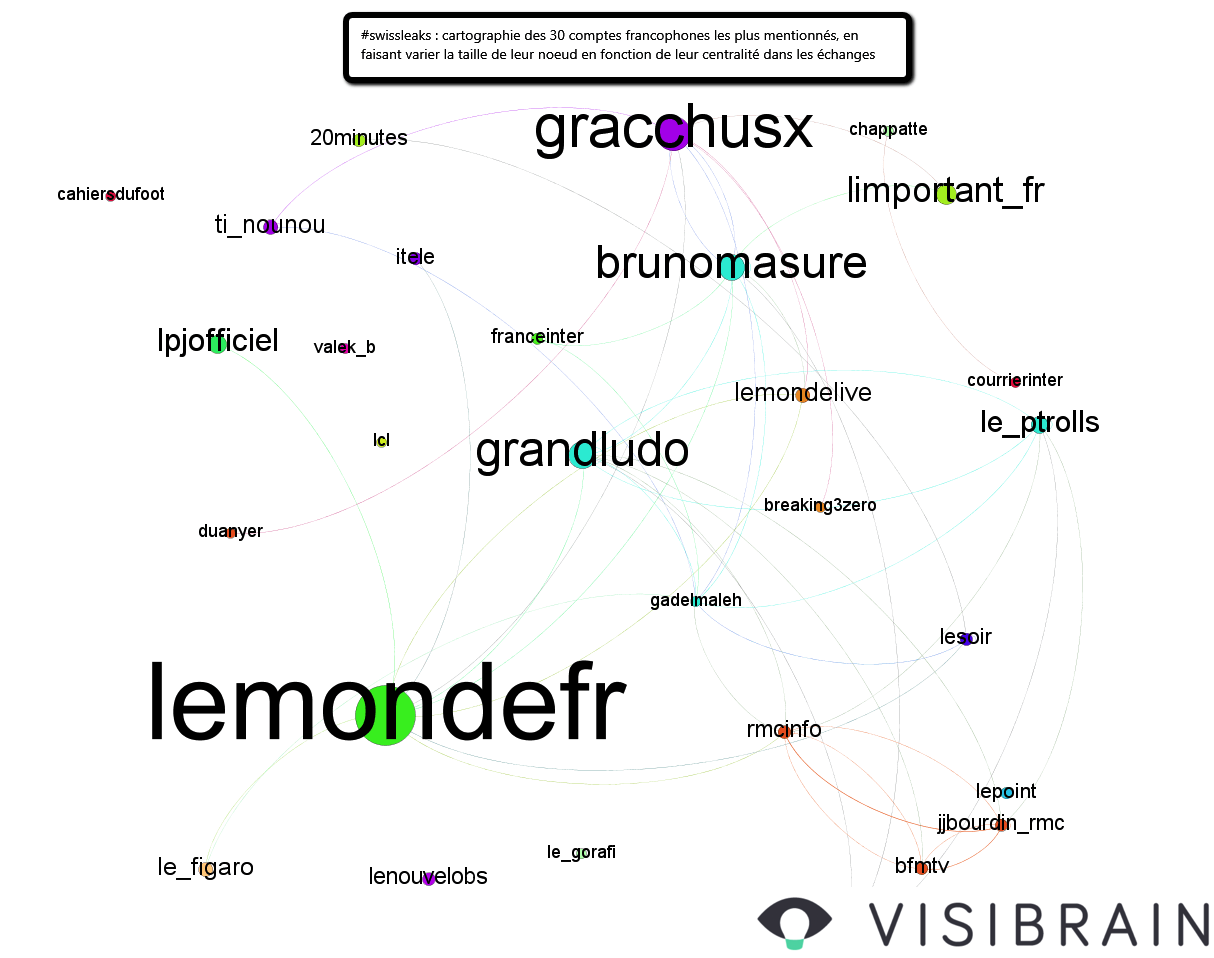
La cartographie du croisement des informations « mentions / degré » et « centralité / betweeness » nous indique que si @gadelmaleh a beaucoup de mentions, il a une faible centralité dans le réseau : les connections ne passent pas par lui, et c’est bien normal, puisque l’acteur est mentionné à l’insu de son plein gré !
A l’inverse, on constate que le compte @gracchusX, qui est très visible sur la deuxième cartographie, a donc un fort score de betweeness centrality, sans être énormément mentionné : il sert de passerelle avec une communauté spécifique.
On peut également, sous réserve de disposer d’un fichier enrichi, ajouter autant de filtres qu’il y a de données à comparer.
Visibrain propose des exports enrichis
- Pour les liens : type de tweet (mention, réponse, RT) ; date du tweet ; nom de domaine d’une éventuelle URL présente ; hashtags utilisés : coordonnées du tweet (si géolocalisés – latitude et longitude) - Idem pour les posts Instagram
- Pour les noeuds (comptes twitter ici) : nombre d’abonnés, nombre d’abonnements, total de tweets, total de favoris, location, date de création du compte… - Idem pour les comptes Instagram
A noter que pour tirer profit de ces informations supplémentaires, il faut préciser en les important leur type : texte, nombre, données temporelles … et les filtres de Gephi s’adapteront en conséquence.
Cela permet d’effectuer des analyses très précises en intégrant à la fois les calculs de statistiques propres à Gephi et des filtrages liés à la nature des données importées dans Gephi.
Exemple concret
Un exemple concret avec la cartographie des tweets concernant le scandale des frais de taxis de l’ex-directrice de l’INA :
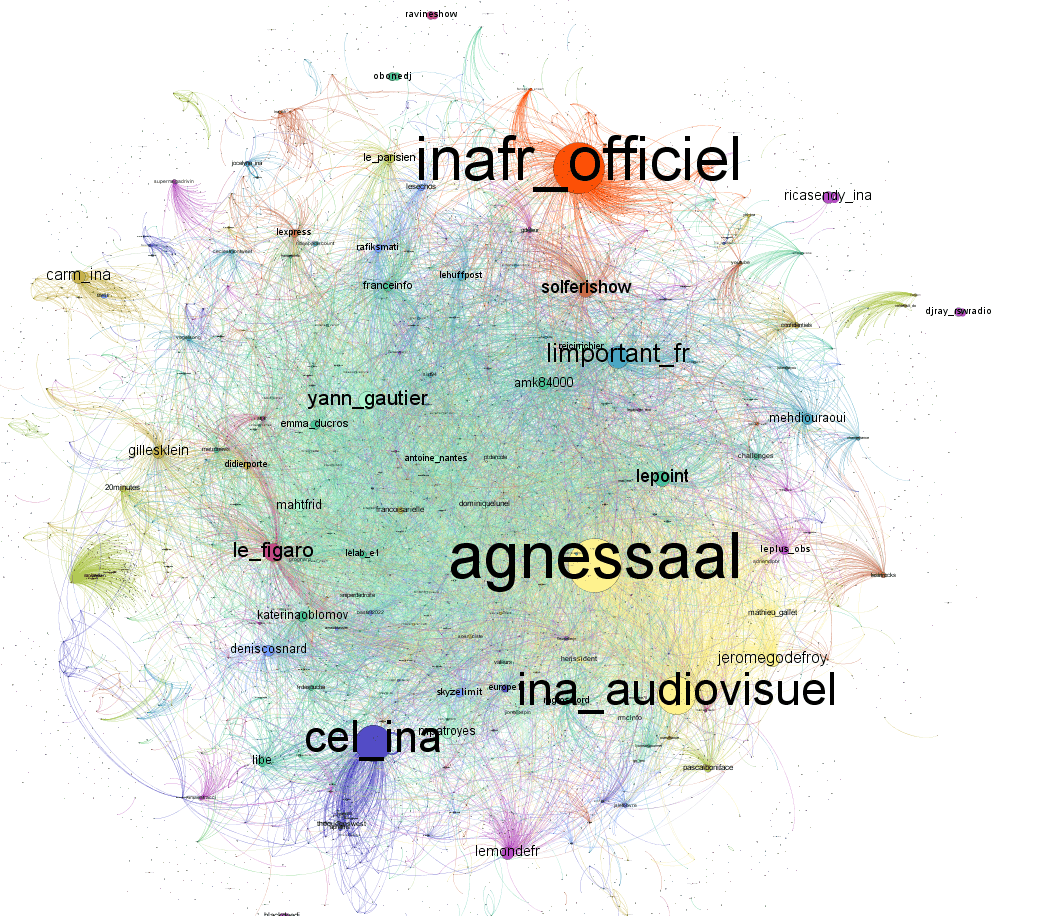
On a ci-dessus la carte des comptes les plus mentionnés. On peut maintenant l’affiner en affichant uniquement les comptes parmi cette cartographie qui ont un nombre important d’abonnés, pour voir si ce sont bien ces comptes qui sont à l’origine du buzz :

On voit bien que les comptes avec le plus d’abonnés ont très peu contribué à la propagation du buzz. Ce sont principalement des médias qui ont repris l’information sans en être à l’origine.
Il est également possible de filtrer les labels des noeuds affichés dans l’export d’une cartographie, afin de la rendre plus lisible :
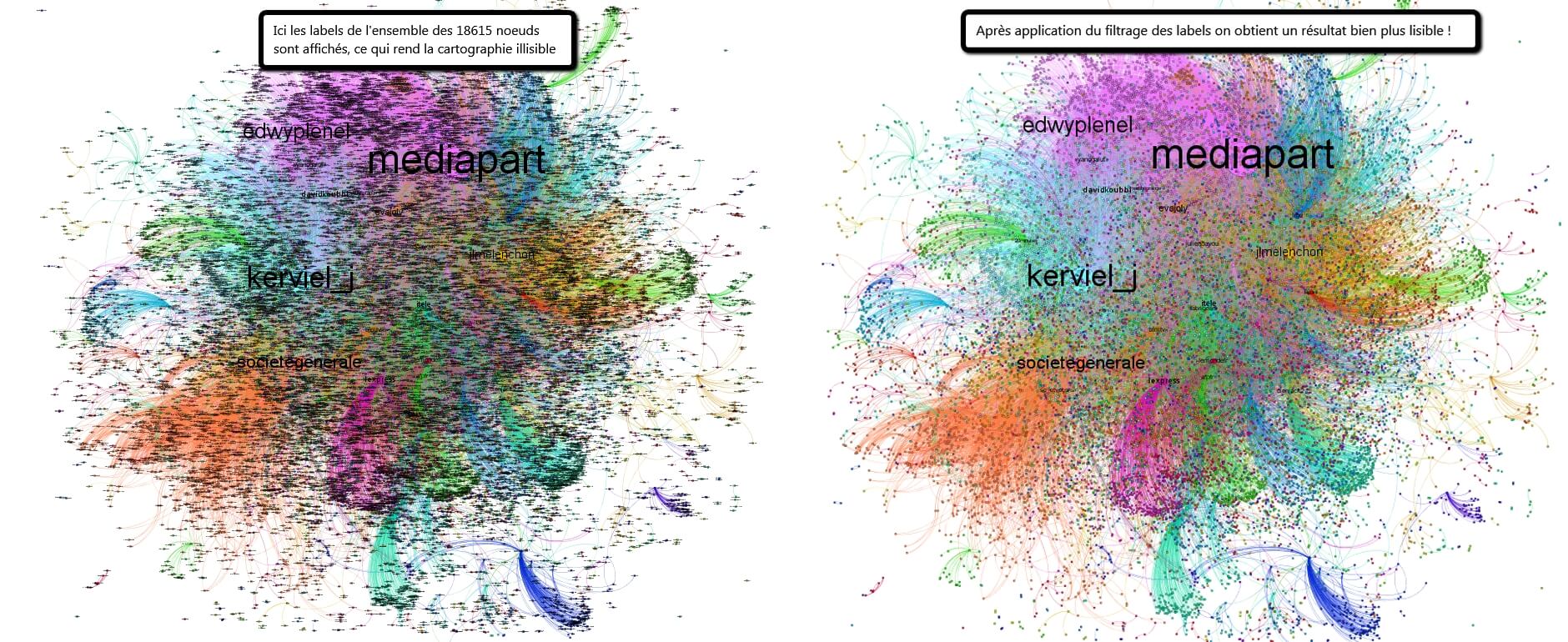
La procédure est assez simple à mettre en place. Après avoir choisi un filtre sur Gephi et validé l’affichage des labels sur l’espace de travail, il suffit de sélectionner une plage de valeurs (et non de la “filtrer”) puis de cliquer sur le masquage des labels hors de la sélection :

Updated over 5 years ago
